Non-Cryptographic Hashing

Hashing functions have wide ranging uses in computing - from helping you find closest businesses around you, to making sure your passwords do not get compromised even if they fall into the wrong hands.

Hash functions, simply, are functions that convert one value into another. For example, consider the following function

def simplest_hash_function_ever(input_string: str) -> str:
    time_now = datetime.now().strftime("%H:%M:%S")
    return input_string + '_' + time_now

All this function does is, appends current timestamp to the given string. Here is what this code will output for hi:

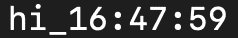
There is not much value this function provides except generating a different output for the same string depending on time of the day - but if we can add some properties to our hash functions we can start seeing their value in computing.

Hash Function Properties

Creating a new hashing algorithm is a non-trivial task. It takes complex math and rigorous testing. Fortunately, there are quite a few hashing algorithms we can use out of the box - with implementations available in most programming languages. Which algorithm to use usually depends on your requirements.

Let’s take a look at some of the common properties non-cryptographic functions have, to derive most value out of them

Our hash function should be deterministic:

If for a given input we can guarantee that we will always have the same output, we get reliable behavior from our function. In the previous example - when you pass in hi, the output value will be different, depending on the time of the day (up to a second) - but if we were to rewrite our hash function such that the string hi always results in the same output we can create reliable mapping between an input string and it’s output.

For it’s application consider a hashtable (or in simpler terms: a lookup table). When a user inputs a string, we pass it through a hash function, which gives us a reliable output. Imagine we want to build a simple lookup table where given a user’s email address, we return their age on file in our system. If we have just one user in our system this will be a simple operation that can be performed in O(1) but if we had millions of users in our system we would have to iterate over our list of a million entries until we find the value we were looking for (barring using any binary search algorithm) - in the worst case, we will not find that email id in our system after iterating through a million entries, making in an O(n) operation. This is where hashtables could be useful.

For this example I am going to cheat and utilize an existing hashing function called md5

Following function will create an md5 hash for each of our email addresses

def hash_me_bro(email_id: str) -> str:
    h = hashlib.md5(email_id.encode()).hexdigest()
    return h

Regardless of how many times you call this function with a particular input the output will always be the same

Passing hi to this function twice will yield the same value

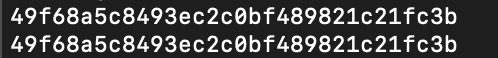
Let’s finish implementing our simple hash table

def find_my_index(email_id: str) -> int:
    return int(email_id, 16) % 100
hash_table = [-1 for i in range(100)]
def save_age(age: int, email_id: str):
    my_hash = hash_me_bro(email_id)
    index = find_my_index(my_hash)
    hash_table[index] = age
def find_age(email_id: str) -> int:
    my_hash = hash_me_bro(email_id)
    index = find_my_index(my_hash)
    return hash_table[index]
save_age(23, 'user1@email.com')
save_age(24, 'user2@email.com')
save_age(25, 'user3@email.com')
print(find_age('user1@email.com'))
print(find_age('user2@email.com'))
print(find_age('user3@email.com'))

To explain this code a bit - we created a hash function to generate a unique(-ish) hash for each email id. We also created a list of 100 items - these will be our partitions. Each index will store age of one of our customers. Every time we get an email address as an input, we can reliably generate a hash and convert it to an integer value between 0 & 100. The resulting integer value will be the index where we will store age for this particular email id.

When we have to retrieve the value, we pass in the email address which will go through the same process of hashing and giving us the exact index of the list which stored age for that particular email address.

Running this code yields the following output

23
24
25

Each of these lookups were constant time, we did not have to iterate over the list to get to the index we were looking for. The formula gave us the exact index to look at to retrieve the value we were looking for.

Note: There is a bug in this code - which we will get to later

Our hash function should be collisions resistant:

A collision is what happens when two different inputs to the hash function result in the same output. If hash values of two email ids are the same; our example in the previous section will have a major flaw - one email id’s hash value will overwrite hash value of the other email id. To top it off we have 100 partitions, so collision is inevitable if we are expecting more than 100 values

To avoid cases like these hash functions try to reduce probability of a collision. High collisions make you reduce the gains made through hash functions. We can avoid the overwriting problem by replaciing the list of integers with a list of list - we can have multiple values on each index - while that resolves one of our problems, there is another problem. If we have high number of collisions we end up coming to the same index and iterating a long list again, hence reducing the search gains made in the previous example.

It will look something like this

As you can see the items are not evenly distributed, as more values are skewed towards the first key, so finding a value from an input that results in hash key 1 will be considerably slower than for other keys. This is a two part problem: collision rate is high and the items are not evenly distributed.

Consider creating a hash of an article that is published. If you are guaranteed uniqueness, anytime a change is made to that article the resulting hash will change. If someone makes a prediction - and later changes their prediction after the event has occured, their original hash will also have changed.

Low collision hashing algorithms like SHA-1 are widely used by source control systems like git to keep track of your changesets.

While we will look at distribution of a hash function next, we can conclude that a good hash function will need to have a low probability of collisions, reducing chances of distinct inputs resulting in the same hash value.

At this point you should be able to see major flaw with our hashtable implementation. To not overwrite any value we need to restructure our hashtable such that each index behaves as a ‘bucket’ - so in case of collision we can add age of the new user to the right bucket along with information required to retrieve it when needed.

A somewhat naive implementation, for the purpose of this post, would look something like this

hash_table = [list() for i in range(100)]
class HashT:
    def __init__(self, email_id: str, age: int):
        self.email_id = email_id
        self.age = age
    def get_email(self):
        return self.email_id
    def get_age(self):
        return self.age
def save_age(age: int, email_id: str):
    my_hash = hash_me_bro(email_id)
    index = find_my_index(my_hash)
    hash_table[index].append(HashT(email_id, age))
def find_age(email_id: str) -> int:
    my_hash = hash_me_bro(email_id)
    index = find_my_index(my_hash)
    for item in hash_table[index]:
        if item.get_email() == email_id:
            return item.get_age()
    return -1

Our hash values should be evenly distributed

Low collisions are important to avoid overwriting values but if you have a finite set of partitions, we also want to make sure all our hash values get evenly distributed across paritions. In our example from before, we would want all our email addresses to be uniformly distributed across the list so the data is not skewed. This is a very important feature of a hash function and is widely used in computing. To highlight why this is important consider following examples

1. Hash tables are the first thing we talked about so it makes sense to list them as the first major application of hashing. You can build hashtables with even distribution to ensure no one partition gets overloaded with most values, therefore keeping your worst lookup time considerably decent. If your hash values are not evenly distributed, one key might get multiple values stored against it while other keys never get used at all.

2. Distributed Messaging Systems use hashing functions to evenly distribute messages across partitions. For example, if you are using kafka as a message broker, you will have a finite set of partitions. Every message will get delivered to a particular partition that the consumers will read data from. If the message distribution is not even, you will end up putting more load on one partition slowing down consumers for that one partition only, while resources on other partitions will go unused.

3. A/B Testing is another great real-world example. If you want to test out a small feature only on a subset of your customers, you can use a hash function that has fairly even distribution, using that to bucket customers into any grouping you want

Hash Functions And Cryptography

The properties we talked about - deterministic, distributed and collision resistant - are not the only properties that are usually associated with hash functions. Hash functions also play a critical role in cryptography. Cryptographic hash functions have a few more additional properties to ensure security.

1. They are one-way hash functions and hard to reverse engineer i.e. from a given hash it is almost impossible to find the input that resulted in that hash value (almost impossible here is due to computation constraints and not necessarily a mathematical impossibility - more details in a separate post one day)

2. It should not be trivial to guess a hash value given an input - you should not be able to precompute what a hash value will be of a given input.

3. Small change to an input results in a vastly different output - i.e. there is no correlation between two almost similar strings

4. Ideally no two inputs should have the same hash value - this is rephrasing of collision resistance but cryptographic hash functions are used with methods like salting to have even similar inputs generate different outputs in a deterministic way (perhaps a topic for another day)

Another shared property between cryptographic and non-cryptographic hash functions is that they should be blazingly fast - so they can be seamlessly integrated into an application.

Cryptographic hash functions are used pretty widely in information security and warrant a post of their own.

What is an ideal hash function then?

An ideal hash function is a function that has no collision - hence guaranteeing the worst case lookup to also be constant time

Hashing is a perfect intersection of mathematics and computer science. This post was, by no means, an exhaustive writeup on cryptography or even hashing - but hopefully could serve as a good introduction to both these concepts.